2018-12-16

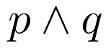
Propositional logic

Logic will get you from A to B. Imagination will take you everywhere
— Albert Einstein

Intro

The use of logic helps us to establish the validity of a given statement. It’s important to notice that a logical statement doesn’t have to make any sense, it only has to be structured following certain rules or formal steps.

There’re two main types of logic systems, propositional logic, and predicate logic. In a propositional system, formal steps make use of propositions sometimes connected with logical operators to make new propositions.

  • propositions: things we want to assess. Statements that can only be true or false.

  • Logical operators: the way the former variables are connected to each other.

This entry will cover the following topics:

Simple propositions

As I was saying a proposition is a sentence that can only represent true or false but can’t represent both at the same time. Examples of this could be:

  • 2 x 2 = 4

  • A Ferrari F450 is faster than a Volkswagen Polo

  • The capital of Spain is Seville

These three statements are propositions. However while the two first propositions are true, and the last one is obviously false.

On the other hand there’re sentences that can’t be considered as propositions because they don’t represent a true/false kind of statements. For example:

  • Are you happy ?

  • Do the right thing!

  • x + y = 2

Complex propositions

We can build up new propositions from pre-existent ones combining them with the use of logical operators. When dealing with complex sequences of statements, instead of repeating all of them all over again, we use variables.

AND

For instance the proposition "The sky is blue and the snow is white" has two parts:

  • p: The sky is blue

  • q: The snow is white

And both parts are combined using the AND operator (∧). Mathematically can be expressed as:

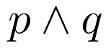
4aa32bf3a4aa6239a102af7635373072.png
Figure 1. and

The use of the ∧ means that the proposition is true when both p and q are true. Another way to represent the possible values for this propositions is using a truth table:

22f8f28238ea878dc92c096384f52043.png
Figure 2. truth table
Here I’m not using the p and q variables in the truth table. However in general I should be using them to keep the verbosity to a minimum.

OR

Now what if we would like to express that some two propositions together are true, if any of them is true. We can express that with the OR operator (∨). Imagine you’re at a raffle, they’re giving away a car, and you and your couple have tickets. I guess, it’s a win whether she/he has a winner ticket or you have a ticket winner. The worst case scenario would be that neither of you have a winner ticket.

Long story short, if we consider p your couple having a winner ticket and q you having a winner ticket, a proposition will be true if any of you have a winner ticket. Mathematically:

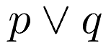
e24a5601777c447da6dcdab4efb64f53.png
Figure 3. or

But, if you would like to go through all the possibilities then you can write down the truth table:

21606cc5359143bb8ba10398d7567961.png
Figure 4. truth table

XOR

Sometimes there could be a situation when we may want to assess that two propositions are incompatible. So the result of that proposition should be true every time one of the propositions is true and the other is false.

Conditional propositions

Conditional statements are a very common form of complex propositions having the form of an hyphotesis followed by a conclusion

Think of conditional statements as if/then type statements.

IF THE NEXT PROJECT USES JAVA, THEN I’M IN

The first thing we should do is to map the expression to propositions or logical variables. Those are the parts of the expression we want to evaluate. In this case we have:

  • A: IF THE NEXT PROJECT USES JAVA

  • B: THEN I’M IN

You can also say that the conditional statement has a hypothesis (IF…​) and a clause (I’m in). We can also notice the dependency between both propositions. A implies that B can happen. This can be expressed as:

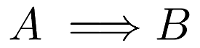
50c8bc1a5046d2c61e4af316a3ce3777.png
Figure 5. implies

Negation

We can also express just the opposite of a given proposition with the negation operator. Lets negate the propositions at hand:

  • !A: IF THE NEXT PROJECT DOESN’T USE JAVA

  • !B: THEN I’M NOT IN

It’s important to notice that here I’m using the ! operator as a conditional variable operator, that’s because most of the time we programmers use it to negate boolean expressions. However the mathematical symbol of boolean negation is ¬.

So how the statement looks like with its propositions negated ?

7d7d1fdf66bb95d608df4f75c4fb7645.png
Figure 6. negation

Which leads me to the next concept, the contrapositive of the initial statement.

Contrapositive

What if I would like to represent the same statement in a negative way:

IF THE NEXT PROJECT DOESN’T USE JAVA, THEN I’M OUT

This would imply that I didn’t join the project, because the next project is not using Java.

7d7d1fdf66bb95d608df4f75c4fb7645.png
Figure 7. contrapositive

This is the contrapositive version of our initial statement. In logic a conditional statement and its contrapositive are logically equivalents, meaning that that both try to express the same thing but from different perspectives, positive and negative. In mathematical syntax:

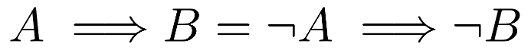
798c57e9c0d61965f651e302b5fb2cb1.png
Figure 8. implies vs contrapositive

Biconditional

Lets remind our initial propositional sentence: IF THE NEXT PROJECT USES JAVA, THEN I’M IN. What if I also say:

IF THE NEXT PROJECT USE PYTHON, THEN I’M I’M

Am I saying something contradictory to the previous sentence ? Not at all. I could be interested in a project using Python or Java. So if I wanted to be very explicit about the fact that I’m willing to do the next project only if Java is on the table, then I have to express the statement using the biconditional operator.

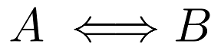
5b82cec87b8710817fbc5922dbc9331b.png
Figure 9. biconditional

This expression now reflects that:

IF, AND ONLY IF THE NEXT PROJECT USE JAVA, THEN I’M IN

So now you’ve narrowed the posibilities of interpretation of your initial proposition.

References