2020-07-30

Groovy Shots - Collections - Set Theory

Sometimes I feel like I’m using certain data structures as if they were all the same. But it turns out if you dig a little on the theory of each of them you may realize there’re data structures that fit better than others for a specific type of problems. In this article I’m reviewing some set theory basics with Groovy.

Groovy Shell

To write the examples I’m using the Groovy shell. To start the Groovy shell go to your terminal and start the Groovy shell:

start groovy shell
[user]$ groovysh -q
groovy:000>

I’ve minimized the verbosity of the Groovy shell in the examples by replacing the groovy:000> prompt by just >. Also remember that in the Groovy shell you may not want to use the def keyword to define a variable (here you can see why)

What is a set ?

A set is a well-defined collection of distinct elements. For example, if we define the following set in Groovy:

distinct elements
> A = [1, 1, 2, 2] as Set
> assert A == [1, 2] as Set

The set only cares about distinct elements, repeated elements will be discarded.

On Groovy sets

A Groovy set could be created with the list-like syntax but using coercion to note that it’s a Set. By default if you coerce a list to Set a java.util.LinkedHashSet will be created.

list-like syntax
> A = [1, 2, 3, 3] as Set     // ===> LinkedHashSet
> B = [4, 5, 6] as HashSet    // ===> HashSet
> C = [1, 1, 1, 1] as TreeSet // ===> TreeSet

Anyway you could also create a set like you do in Java:

> A = new HashSet()
> B = new TreeSet()
> C = new LinkedHashSet()

Union, intersection, difference

The first set operation that springs to mind is adding up two sets together. Given a set A and a set B the union of A and B is all elements of A and B.

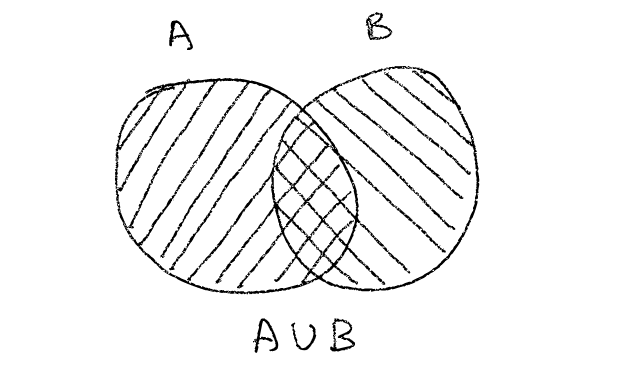
Union

We can use the + operator in Groovy to add one set with another set.

union
> A = ["john", "peter"] as Set
> B = ["anne", "robby", "robby"] as Set // notice I've repeated robby deliberately ;)
> unionAB = A + B
> assert unionAB == ["john", "peter", "anne", "robby"] as Set

If we’d like to know which elements of A are not in B we could calculate the difference between A and B using the - operator:

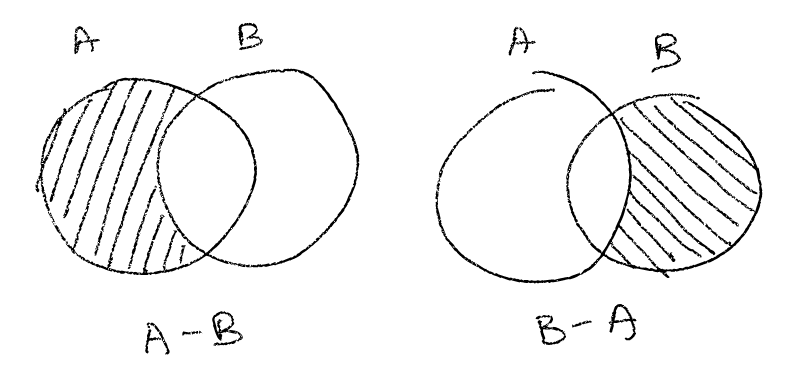
Difference
difference
> A = ["john", "peter", "corie"] as Set
> B = ["anne", "robby", "peter"] as Set
> diffAB = A - B
> diffBA = B - A
> assert diffAB == ["john", "corie"] as Set
> assert diffBA == ["anne", "robby"] as Set

The difference between two sets is also used to introduce the relative complement of a given set. If A - B is everything that is in A that is not in B, the relative complement is everything that is not in A that is in B. Or in plain english, just the opposite. So if the difference between A and B is noted as A - B the relative complement of A related to B is noted B \ A, but effectively is equal to B - A.

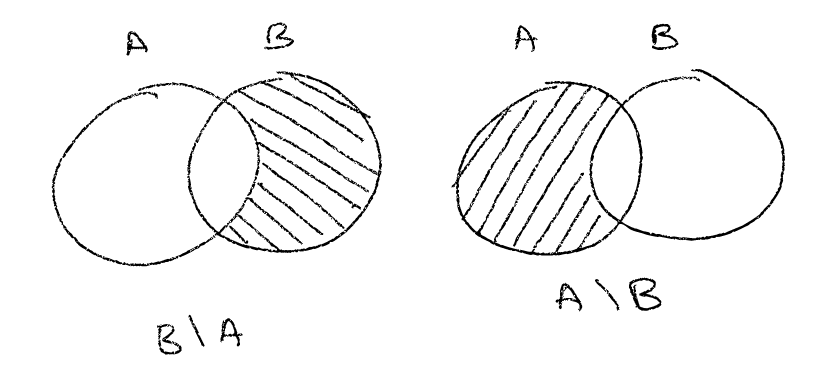
Complement
relative complement
> A = ["john", "peter", "corie"] as Set
> B = ["anne", "robby", "peter"] as Set
> relCompOfA = B - A // ==> A \ B
> assert relCompOfA == ["anne", "robby"] as Set

Why is important to know the relative complement ? It helps you to calculate the symmetric difference.

Symmetric difference

At some point you may want to know all elements of A and elements of B without the elements that are common to both sets. That’s called the symmetric difference between A and B. Basically all you have to do is to sum the relative complement of both sets.

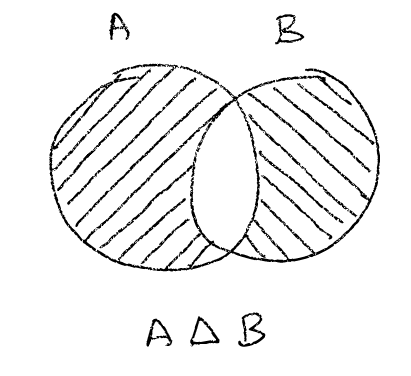
Simmetric

We can create a closure containing the formula of the relative complement and then use it to calculate the simmetric difference.

symetric difference
> A = ["john", "peter", "corie"] as Set
> B = ["anne", "robby", "peter"] as Set
> relComplement = { a, b -> b - a }
> symmetricDiff = { a, b -> relComplement(a, b) + relComplement(b, a) } // ===> (B \ A) U (A \ B)
> assert symmetricDiff(A, B) == ["anne", "robby", "john", "corie"] as Set

Intersection

Another very common problem is to know which elements are shared between sets, or in other words what’s the intersection between them.

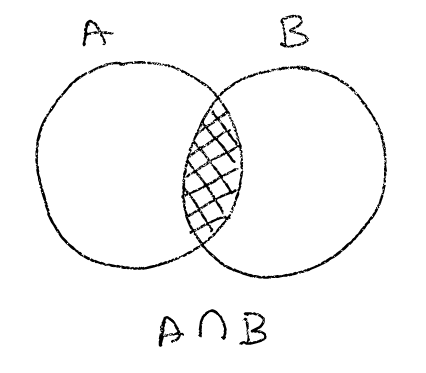
Intersection
intersection
> A = [1, 2, 3, 4] as Set
> B = [1, 3, 5, 6] as Set
> C = [1, 7] as Set
> assert A.intersect(B) == [1, 3] as Set
> assert B.intersect(C) == [1] as Set

The intersection also is an associative and commutative operation:

intersection properties
> assert (A.intersect(B)).intersect(C) == A.intersect(B.intersect(C)) // associative
> assert A.intersect(B).intersect(C)   == C.intersect(B).intersect(A) // commutative

But maybe you are only interested in knowing if two different sets have nothing in common. Then you may want to know if they are disjoint sets.

disjoint
> A = [1, 3, 5] as Set
> B = [2, 4, 6] as Set
> assert A.disjoint(B) == true // A and B have nothing in common

Versions

  • Groovy 2.5.13

References