2020-09-22

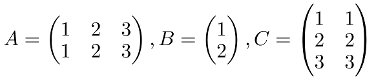
Matrices - Basic operations

After review basic matrix operations in a previous article, in this article I’m reviewing these operations and their properties using Python and the Numpy library.

Matrices with Numpy

Although there’s the matrix function to create matrices, according to documentation is deprecated in favor of array. So lets say we want to create different arrays:

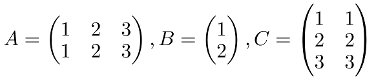
3d2d2ee2baa7a5273daa6bbd5417e412.png
Figure 1. array A

As we’ve mentioned earlier, we need to import Numpy and then create an array representing the matrix. A matrix in Numpy will be written as a multidimensional array:

Matrix declaration
import numpy as np

A = np.array([
    [1, 2, 3].
    [1, 2, 3]
])

B = np.array([
    [1],
    [2]
])

C = np.array([
    [1, 1],
    [2, 2],
    [3, 3]
])

SUM

So, How do we sum two different matrices ? As easy as declaring both matrices and then add them up using the + operator:

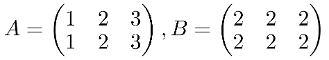
d5de5fdb95dd8655eb0290535b65150f.png
Figure 2. two matrices A and B
adding up two matrices
import numpy as np

A = np.array([
    [1, 2, 3],
    [1, 2, 3]
])

B = np.array([
    [2, 2, 2],
    [2, 2, 2]
])

A + B
Of course if you try to sum two matrices with different order (different shape in numpy terms) the operation will fail, as it’s not possible to sum matrices of different order.

Commutative

With the same matrices we can check that the commutative property holds. We can can use array_equal to make sure both A + B and B + A are equal.

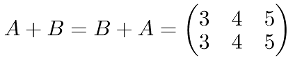
53199ee40c6dcf18bfb0ef8acabcda91.png
Figure 3. commutative
commutative proof
import numpy as np

A = np.array([
    [1, 2, 3],
    [1, 2, 3]
])

B = np.array([
    [2, 2, 2],
    [2, 2, 2]
])

np.array_equal(A + B, B + A)

Associative

Now checking the associative property with a third matrix C:

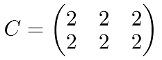
f5a50397d43fbc7d2b1086a959240609.png
Figure 4. another matrix C
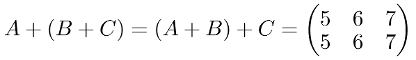
fd801dcd6a6a044ec7b1ad9bf9be2fa1.png
Figure 5. associative
import numpy as np

A = np.array([
    [1, 2, 3],
    [1, 2, 3]
])

B = np.array([
    [2, 2, 2],
    [2, 2, 2]
])

C = np.array([
    [2, 2, 2],
    [2, 2, 2]
])

np.array_equal(A + (B + C), (A + B) + C)

Additive identity

Finally if we add the zero matrix to A it should return the A matrix: You can create a zero array using Numpy’s zeros function.

THe zero matrix should be of the same order as A. Meaning if A is of order 2x3 then the zero matrix should be of order 2x3 as well.
adding zero matrix to A
import numpy as np

A = np.array([
    [1, 2, 3],
    [1, 2, 3]
])

O = np.zeros((2,3))

np.array_equal(A + O, A)

Additive inverse

Given a matrix A there is its inverse -A so that -A+A=O. Adding up a matrix and its inverse results in a zero matrix.

additive inverse proof
import numpy as np

A = np.array([
    [1, 2, 3],
    [1, 2, 3]
])

O = np.zeros((2, 3))

np.array_equal(A + (-A), O)

MULTIPLICATION

Matrix multiplication is also known as the dot operation, and there’s the dot function in Numpy for a given matrix. Therefore for multiplying two different matrices we can use this dot function:

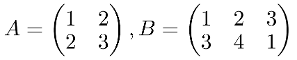
aca54a4709a9031e9213018f31e2e5f3.png
Figure 6. two matrices A and B
multiplying A * B
import numpy as np

A = np.array([
    [1, 2],
    [2, 3]
])

B = np.array([
    [1, 2, 3],
    [3, 4, 1]
])

expected = np.array([
    [ 7, 10,  5],
    [11, 16,  9]
])

np.array_equal(A.dot(B), expected)
Again both matrices must be compatible in order to multiply them, otherwise an error will be raised.

Associative

We’re checking that A(BC) = (AB)C.

Remember that the order of the elements in matrix multiplication is important, meaning ABC != CBA:
associative proof
import numpy as np

A = np.array([
    [2, 2],
    [2, 2],
])

B = np.array([
    [1, 2],
    [1, 2],
])
C = np.array([
    [2, 1],
    [2, 1],
])

BC = B.dot(C)
AB = A.dot(B)

np.array_equal(A.dot(BC), AB.dot(C))

Distributive

The distributive property has two parts, A(B+C) = AB + AC:

A(B + C) = AB + AC
A = np.array([[1, 2], [1, 2]])
B = np.array([[2, 2], [2, 2]])
C = np.array([[3, 3], [3, 3]])

AB = A.dot(B)
AC = A.dot(C)

np.array_equal(A.dot(B + C), AB + AC)

And then (A + B)C = AC + BC

(A+B)C = AC + BC
A = np.array([[1, 2], [1, 2]])
B = np.array([[2, 2], [2, 2]])
C = np.array([[3, 3], [3, 3]])

AC = A.dot(C)
BC = B.dot(C)

np.array_equal((A+B).dot(C), AC + BC)

Multiplicative identity

Multiplicative identity property says that if any matrix A is multiplied by the identity matrix then the result will be A. You can use numpy’s function identity to get an identity matrix:

multiply by identity
import numpy as np

A = np.array([
    [2, 2],
    [2, 2],
])

I = np.identity(2)

np.array_equal(A.dot(I), A)
np.array_equal(I.dot(A), A)

Resources