2020-09-21

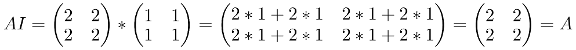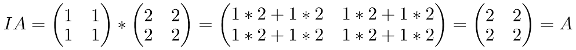
Matrices - Basic operations

Matrices are one of the most used Math abstraction nowadays, specially in the field of machine learning. That’s why I encounter myself lately reviewing matrices theory. Now with the most basic operations: sum and multiplication.

SUM

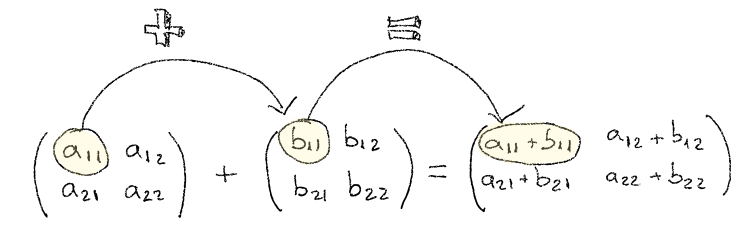
Before adding up two matrices they must have the same dimensions, the same number of lines and columns. Once we’ve got two valid matrices, we have to add up each correspondent pair of both matrices, a1,1 + b1,1, a1,2 + b1,2 …​ an,m + bn,m.

commutative
Figure 1. Sum (row,column) of A with the same (row, column) of B

So, lets say we have a matrix A and a matrix B and lets add them up:

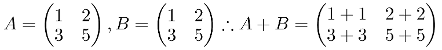
4c27af57175b6e8c9e1e83b967f5ede3.png
Figure 2. Adding up two matrices

Matrix addition has a number of properties worth knowing, such as: commutative, associative, the additive identity and the additive inverse.

COMMUTATIVE

If A and B are matrices of the same order then it doesn’t matter the order in which you add them up, in other words A + B = B + A. Lets prove it, lets make A and B to be two real matrices:

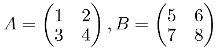
92dfbc2cb02304b93145c3469c378f12.png
Figure 3. Two matrices of the same order

So lets do A + B and then B + A to check that both operations have the same result:

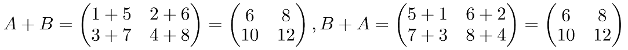
b87ad35c27e48900c7866490787ad4c0.png
Figure 4. Commutative property proof

ASSOCIATIVE

Matrix addition is associative. This says that, if A, B and C are Three matrices of the same order then you will get the same result whether you add A to (B + C) or (A + B) to C. Lets prove it by defining three matrices:

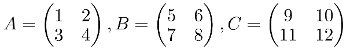
2a51117b88e4737630b7b005409604e7.png
Figure 5. Three matrices of the same order (2x2)

Now lets define B + C AND A + B:

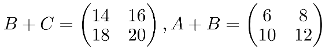
d05998e5da9797d13c9909bdcf483c89.png
Figure 6. Resolving (B + C) and (A + B)

Finally:

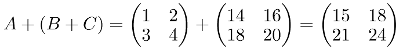
bc4fdc58b112103ec89267fed60e6d9e.png
Figure 7. Associative property proof A + (B + C)
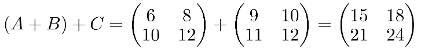
3ba1da5d60495d608982f8fbf8d5f8e4.png
Figure 8. Associative property proof (A + B) + C

ADDITIVE IDENTITY

Let A be the matrix then, A + O = A = O + A Therefore, O a matrix of the same order as the matrix A that when added up to A equals to A as well. O is also named the null or zero matrix. So lets prove it adding up a matrix A with a compatible zero matrix. First the two matrices:

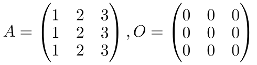
4961332eccb32f8020b94d816e233840.png
Figure 9. Two matrices of the same order (3x3)

Now adding up A to O must result in A:

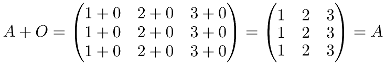
71be61798e5508737ee1b5c54b988c61.png
Figure 10. Additive identity proof

ADDITIVE INVERSE

Let A be the matrix then, A + (- A) = O = (- A) + A where -A is the inverse of A. The inverse of a matrix is the matrix obtained by changing the sign of every matrix element. Having A and -A:

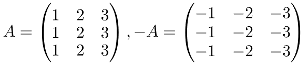
4fbcffb55906329dd3249da3f3aefa75.png
Figure 11. Matrix A and its inverse -A

So basically adding up -A to A will end up giving O (the null matrix):

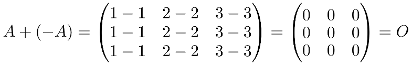
9d05f9c5183afc6cad849907627d84d4.png
Figure 12. A + (-A)

And the opposite works the same:

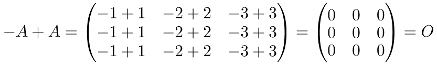
8c3aa1abda55989b4d89bec201cd34b9.png
Figure 13. Additive inverse proof

MULTIPLY

If A is a matrix of order m x n and B is another matrix with order o x p where m and o are number of rows and n and p are number of columns, in order to be able to multiply A x B, then n == o must be true, meaning that the number of columns of A must be equals the number of rows in B, and the resulting matrix will be of order m x p:

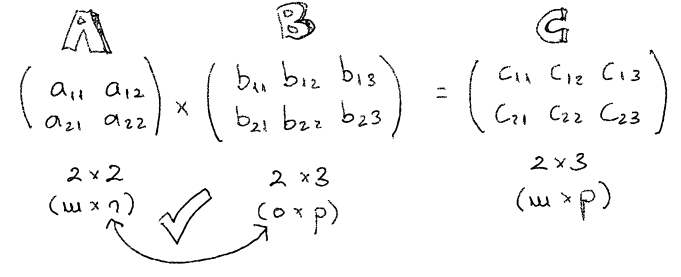
multiplication

How is the procedure of multiplying two matrices ? Well, the element Ci,j (where i is the row and j is the column) will be the result of multiplying the elements of Ai by the elements Bj and adding up their results. So for example, when multiplying A x B = C:

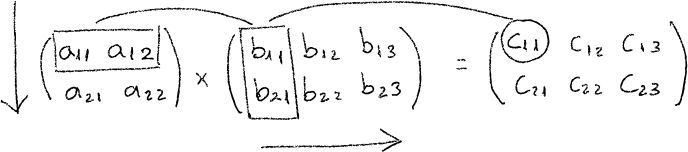
process
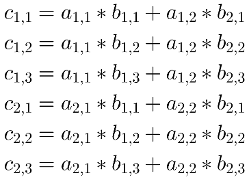
e29b866254e91513ccd25ce45adbdeaa.png
Figure 14. Matrix C cells

Here’s an example, there’re two matrices A and B:

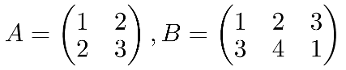
1f715b76e89b3d4ece10306a4dca1849.png
Figure 15. Two matrices to multiply

Then in order to get c1,1 we need to multiply elements from a1,…​ and b…​,1 and then add them up:

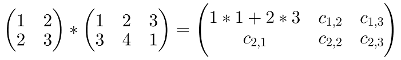
2b7916ac4fd6b1ac6271bf772400748a.png
Figure 16. Resolving c1,1

Now in order to get c1,2 we need to multiply elements from a1,…​ and b…​,2:

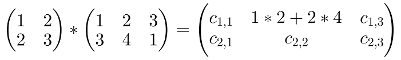
42da6e8bbee0c4f3de8531300e6f24fd.png
Figure 17. Resolving c1,2

And this would go on and on for remaining cells:

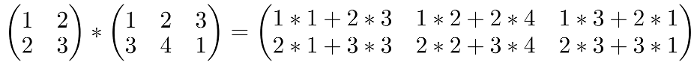
d229eb831653e78bbc39dde22f0caf09.png
Figure 18. Two matrices to multiply

Finally simplifying:

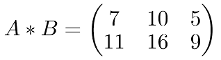
5a3a9caf2641b93284b40105c62d6038.png
Figure 19. A * B result

The matrix multiplication has a few properties: the associative the distributive and the multiplicative identity. Lets view them all with examples. I’m using the following matrices:

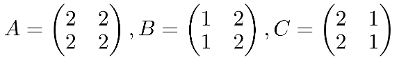
11393696767fea805a3d694a125971e0.png

Associative

This should be called pseudo-associative due to the fact that the order to the elements in a matrix multiplication matters. AB and BA may not result in the same solution.

The associative property says that A(BC)=(AB)C. So lets calculate A(BC) first and then (AB)C and compare both results:

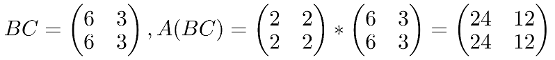
b470aa8be45237e4c1b2b352a961222c.png
Figure 20. A(BC)

Then A(BC):

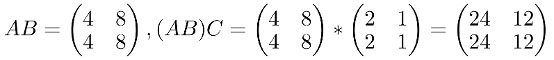
9c2403f161ed4dd7739846572f75b2b0.png
Figure 21. (AB)C

Distributive

When multiplying three different matrices A, B and C the distributive property says that A(B+C) = AB + AC and also that (A+B)C = AC + BC. So again having the previous A, B and C matrices, lets do a couple of calculations:

A(B+C) = AB + AC

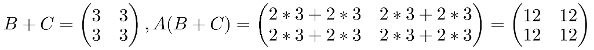
052d2910493fa9d578b5daf39dfca2d9.png
Figure 22. A(B+C)
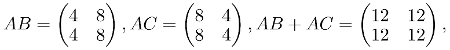
6c5a38b2aed9a001b2b85ef8e3e4a370.png
Figure 23. AB + AC

(A+B)C = AC + BC

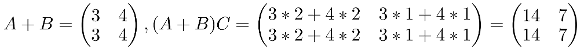
7b2e6d43d39332682192f0a0738c8fc6.png
Figure 24. (A+B)C
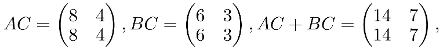
8572889475f81f70c1cf6cf3bb230f27.png
Figure 25. AC + BC

Multiplicative identity

The multiplicative identity property says that there’s an identity matrix. When a matrix is multiplied by this identity matrix the result is the matrix itself. The mathematical formula would be AI = A = IA where I is the identity matrix.

12688282ae1a31faf6f26e990231805d.png
Figure 26. multiplicative identity proof (AI)
a34c7c0b6195377908a7c080296062f8.png
Figure 27. multiplicative identity proof (IA)