2021-02-10

Imbalanced classes

Accuracy is not always what you think

Most of the time I’m focusing on getting the highest score when training my machine learning models. Lets remember the definition of accuracy: The number of predicted samples that were correctly labeled divided by the total number of samples.

Figure 1. accuracy formula

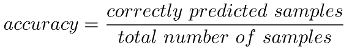
But what happens (imagine we’re in a binary classification problem) and there are many samples labeled with a possitive class or the other way around, How that situation could affect the score? Moreover, What the score would mean in these situations ?

To dig a little bit into that I’m creating a classification model with the Haberman’s Survival Data Set which contains cases from a study that was conducted between 1958 and 1970 at the University of Chicago’s Billings Hospital on the survival of patients who had undergone surgery for breast cancer. This dataset is available from the UCI Machine Learning Repository.

Loading data

import pandas as pd

df = pd.read_csv("haberman.data", names=['age', 'year', 'aux_nodes', 'status'])
df.head()

I’d like to train a classifier to choose between target values (possible values in the status column):

1: the patient survived 5 years or longer
2: the patient died within 5 year

The firts classification uses a support vector classifier (SVC) and I’m getting the following score:

Classifying with SVC

from sklearn.model_selection import train_test_split
from sklearn.svm import SVC

features = [col for col in df.columns.values if col != 'status']

X = df[features]
y = df['status']

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 0)

svc = SVC().fit(X_train, y_train)
svc.score(X_test, y_test)

accuracy

0.5974025974025974

Hold on a second. Is this the best I could do ? Well, there’s the concept of a baseline model. You can think of the baseline as the worst possible classificator you could come up with. In other words I should always come up with something better than the baseline model. If not, my model is as useful as tossing a coin.

In Scikit you can create a baseline classification model using the dummy classifier. I’m creating a baseline for my dataset:

Using DummyClassifier for the baseline

from sklearn.dummy import DummyClassifier

dummy = DummyClassifier(strategy = "most_frequent").fit(X_train, y_train)
dummy.score(X_test, y_test)

accuracy

0.5974025974025974

Why am I getting the same score ? There could be several reasons why my classification model is scoring as bad as the dummy classifier:

Imbalanced class
Innefective, erroneous or missing features
Poor choice of kernel or hyperparams

If my model performs almost the same as the baseline model, it could be considered as good as tossing a coin.

For the shake of the article, lets say I suspect my dataset is imbalanced. How can I be sure that’s the case ?

Checking the percentages of each target class

def show_balance(dataframe):
    rates_df = dataframe[['status', 'age']]\
        .copy()\
        .groupby('status')\
        .count()\
        .rename(columns={'age': 'count'})\
        .reset_index(drop=False)
    rates_df['pct'] = rates_df['count'] / rates_df['count'].sum()

    return rates_df

show_balance(df)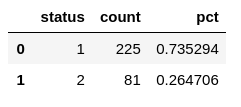

Ok so instead of having the same amount of samples of each target class, I’ve got 73% of class "1" and 27% of class "2", so it’s clearly imbalanced. That situation favors that the dummy classifier because the dummy classifier only classifies correctly the majority class, meaning that 73% of the time would be getting the right outcome.

You may be wondering (I did)… if the majority class is 73% of the samples, then Why the dummy classifier is not getting 73% of accuracy ? The answer is because we’re splitting the samples into training and test sets, and that changes the percentages, decreasing them.

The objective now would be having the same amount of samples for each class. There’re several techniques that can help me mitigating the problem with imbalanced classes. In this entry I’m focusing in two of them:

Resampling the dataset: ways of increasing an under-represented class or decreasing an over-represented target class.
Using penalized models: penalizations applied to models to take into account the under/over representation of a given target class.

To check out more techniques to reduce the impact of imbalanced classes I recommend you to take a look to this wonderful article from machinelearningmastery.com.

Resources

Over-Sampling vs Under-Sampling

In a binary classification problem when you have many samples from one class and very few from the other you can choose between:

Over-Sampling: Create more samples from the under-represented class
Under-Sampling: Reduce the number of samples from the over-represented class

In any case the optimal situation would be to have both classes equally represented. There’re a couple of things worth mentioning when trying to decide whether to choose one technique or the other:

Use under-sampling when you have a big dataset
Use over-sampling when you have a small dataset

In the dataset I’m working on, the problem is that there’s not much data, just 300 samples, it doesn’t make sense to reduce even more the dataset by under-sampling the over-represented class. Therefore I’m going to over-sampling the under-represented class. To do so, I’m adding to my toolbox the https://imbalanced-learn.org library, which is an add-on to the scikit-learn framework focused (as the name implies) on dealing with imbalanced classes.

To install a Python library in my Jupyter notebook using pip I followed the instructions found at https://jakevdp.github.io/blog/2017/12/05/installing-python-packages-from-jupyter/

installing imbalance-learn in my jupyter notebook

# Install a pip package in the current Jupyter kernel
import sys
!{sys.executable} -m pip install -U imbalanced-learn

Then I applied the over-sampling strategy over my dataset. You don’t have to tell the library which target class is under-represented, the algorithm figures it out. As a result the execution it returns the new resampled X and y.

over-sampling under-represented class

from imblearn.over_sampling import SMOTE

smote = SMOTE()
X_resampled, y_resampled = smote.fit_resample(X, y)

Now both target classes should be even:

show classes new balance

new_df = X_resampled.copy()
new_df['status'] = y_resampled.copy()

show_balance(new_df)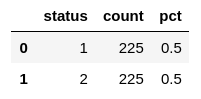

Then I can start using the new resampled dataset to create the new training/test sets.

creating the new TRAINING/TEST sets

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X_resampled, y_resampled, random_state=0)

Follow up I’m applying the new training/testing datasets to the baseline:

baseline resampled

from sklearn.dummy import DummyClassifier

dummy = DummyClassifier(strategy = "most_frequent").fit(X_train, y_train)
dummy.score(X_test, y_test)

resampled dummy score

0.48672566371681414

Now the score is lower than before and close to the 50%. That makes sense due to the fact that now both target classes are even and there’s no target class more predominant than the other.

But the most important thing is to check how the SVC classificator is now performing:

resampled SVC model

from sklearn.svm import SVC

svc = SVC().fit(X_train, y_train)
svc.score(X_test, y_test)

resampled SVC score

0.6283185840707964

Well is performing slightly better than before, and it’s performing way better than the baseline.

All target classes should be equally represented

Resources

Penalized models

Another technique is to tune machine learning algorithms to make them aware of the target class imbalance. Lets get the initial imbalanced train/test sets.

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

Now using SVC I’m telling the algorithm to be aware of imbalance classes:

tuned SVC

from sklearn.svm import SVC

# https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html
svc = SVC(class_weight='balanced').fit(X_train, y_train)
svc.score(X_test, y_test)

score

0.6363636363636364

And the same goes with LogisticRegression:

tuned LogisticRegression

from sklearn.linear_model import LogisticRegression

# https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html
logistic = LogisticRegression(class_weight='balanced').fit(X_train, y_train)
logistic.score(X_test, y_test)

score

0.6493506493506493

According to the Scikit documentation the “balanced” mode uses the values of y to automatically adjust weights inversely proportional to class frequencies in the input data as n_samples / (n_classes * np.bincount(y)). You can also tune it manually passing the weight associated with classes in the form {class_label: weight}.

It seems that a general rule of thumb could be using the inverse of the class distribution present in the training dataset. In the example class "1" had 73% and class "2" had 27%, so if we inverted the weights:

manually tuned

from sklearn.linear_model import LogisticRegression

# https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html
weights  = {1: 0.27, 2: 0.73}
logistic = LogisticRegression(class_weight=weights).fit(X_train, y_train)

logistic.score(X_test, y_test)

As expected I’m getting a similar score:

score

0.6493506493506493